Into and out of
Rotations in hyperspace
Augmented reality artwork by Daniel Jackson for Inscription journal, issue 3: Folds

Inscription symposium for Issue 3 at Tate Britain, 25th November 2022
14.00 - 14.20 Daniel Jackson and Ian Truelove, folding in eleven dimensions.
‘Into and out of’ is an augmented reality artwork triggered by the image ‘Bottari’ by Kimsooja on the cover of Inscription journal, issue 3: Folds. The artwork presents a rotating hypercube locked to the image, with a sequence of related words from 2 groups corresponding to the words from the artwork title ‘into’ and ‘out of’.
On a mobile device you can view the artwork here and trigger it by pointing your camera at the Inscription journal cover. If you do not have a copy of Inscription issue 3, you can point your camera at the Kimsooja image below.
Background: art and technology – experiments with new forms of representation – augmented reality and virtual reality
I have always had an interest in modes of representation in art with respect to how they have evolved throughout history as a direct consequence of our understanding of the world and the development of technology and techniques.
In this project ‘into and out of’ I am revisiting work I undertook for my MA at Middlesex University in 1993.
My thesis ‘Impossible Worlds’ examined the possibilities of the computer as a new, and increasingly accessible, medium for artists. An awareness of Euclidean multi-dimensional geometry at the beginning of the twentieth century had a significant influence on artists at this time (Linda Henderson, 1983). It seemed, in 1993 at the end of the twentieth century, that this curious geometry was a good lens through which to examine how computers could help us represent things which previously we could only conceive of as axiomatic abstractions or view as static drawings.
The practical aspect of the thesis was the software development of a multi-dimensional graphics system for the display and manipulation, through rotation, of n-dimensional hypercubes.
The code was written in C, now a somewhat outdated and complicated programming language, and required powerful and expensive Silicon Graphics computers to display the hypercubes and allow them to be manipulated in realtime. After leaving college and working at a virtual reality company in the mid-1990s it was not so easy getting your hands on these expensive machines and the demands of work and the time required to re-write the software meant that the project I always intended to keep developing became neglected.
29 years later technology has progressed such that the computing power of mobile phones is now equivalent or better than of the rather coveted green and purple Silicon Graphics machines that cost tens of thousands of pounds. The 3D software which I used in the 1990s was called GL – it has kept on evolving becoming OpenGL and now for the internet WebGL – so there has been some consistency.
In some ways we are still at the very beginning of what is possible. VR has been around since the 1990s when augmented reality applications were being used in the military and proposed in other fields. It is only now though that open standards have evolved, the cost of the hardware has dropped and there are cross-platform game development environments; all of which mean that these mediums can be more widely explored and we can develop this new artistic language.
Outline: out of the page, into another dimension
Inscription journal launched with the objective to commission an augmented reality intervention for each issue. This initiative aims to extend the boundaries of the journal into the digital realm.
In the augmented reality artwork ‘into and out of’ there are several colliding realities: the real world viewed through our mobile cameras; the evocation and visual presence of Kimsooja’s ‘Bottari’ image; the virtual representation of the hypercube, an axiomatic curiosity from a higher dimension; and the title (an integral part of the work) with the changing words as a provocation to our imagination.
The folding or turning of the page of the book takes the flat page and rotates it through the third dimension. The 2 dimensional words on the surface of the page transport the reader into another world. Turning the paper page takes the viewer out of the words and then returns them back on completion of this action.
Visualising a hypercube is best achieved by having it rotate around the 6 axes of rotation that exist in 4 dimensions – you get to see how it behaves and gain some insight into its strange form. The act of folding in the physical world takes a 2 dimensional material and bends it, making it smaller. We can consider this folding as an act of rotation because it happens around a line, or we could say around an axis. If extrapolated from 3 to 4 dimensions we realise that this equivalent 4D rotation will happen around a plane.
The title ‘into and out of’ also describes the appearance and disappearance of the 8 cubes that form the hypercube as it rotates around the 6 planes of rotation. The cubes appear as if they are coming ‘out of’ and going ‘into’ each other.

Higher dimensions and Euclidean geometry
Axioms and abstraction
The observable world is clearly 3 dimensional and we know this through our own experience with touch, sight, sound, smell and movement. Conversely some of the techniques we use to describe and map out our 3D world are based on axioms, that is propositions on which abstract structures are defined. The development of the technique of perspective is an example of an axiomatic structure being employed to represent the world in a ‘realistic’ way.
The development of multi-dimensional geometry did not come about until the 1820s when Möbius found that the only way to prove equivalence of 2 mirrored objects was by rotation in the fourth dimension. This problem is best understood by examining the corresponding problem with 2 dimensional mirrored and congruent shapes (Diagram 1). No amount of shifting, shearing or rotation in the 2 dimensional plane will map one of the triangles onto the other. However if the line of symmetry is established it is possible to achieve this if one triangle is rotated through the third dimension around this axis.
Note that this 3 dimensional rotation takes place around a line. In 2 dimensions rotation will occur around a point. In 1 dimension rotation is not possible.
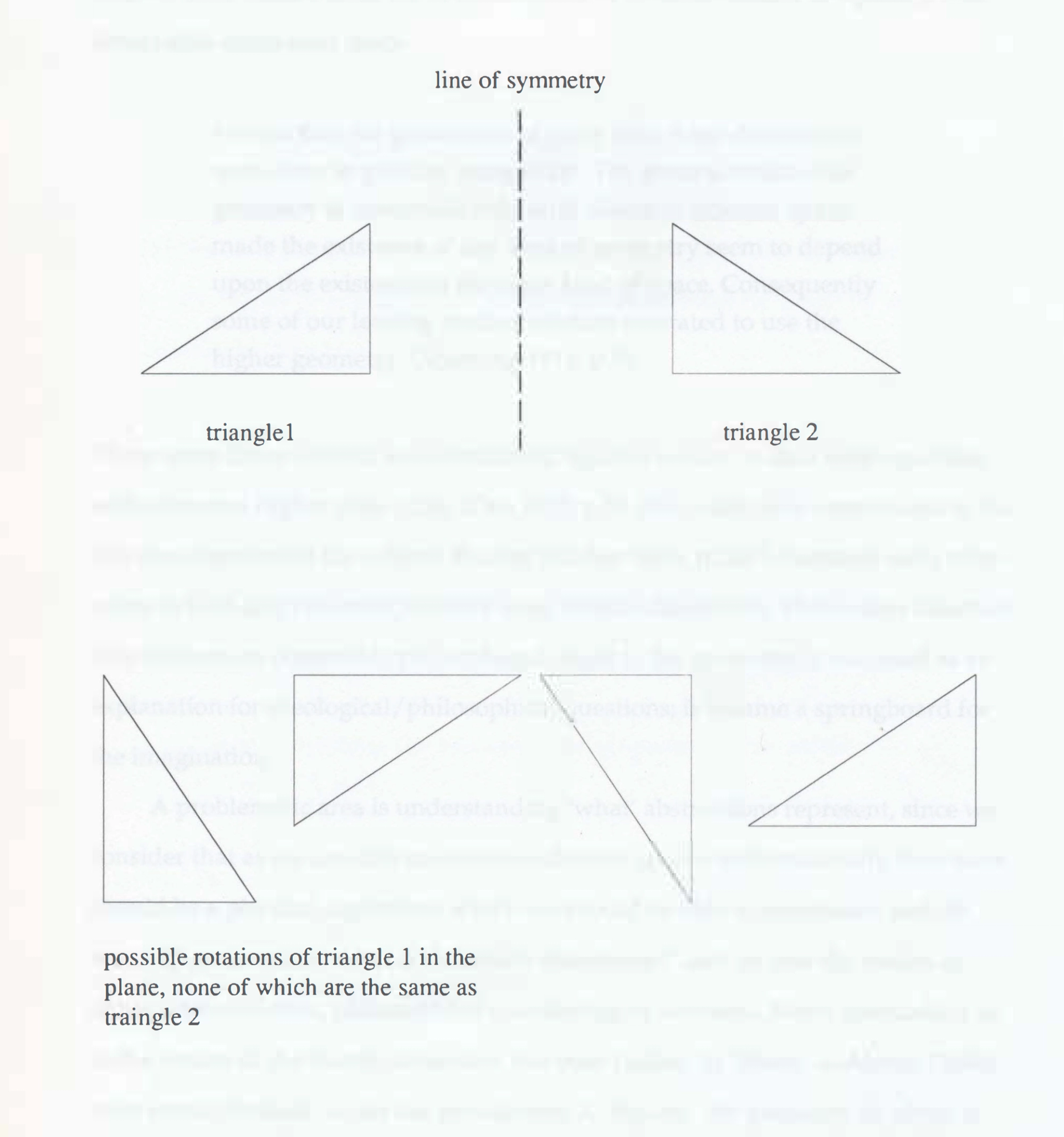
As we have demonstrated making the analogy from one dimension to another is a useful way of understanding how each dimension works. Edwin A. Abbott (1884) in his classic book Flatland under the pseudonym A. Square explores a purely 2 dimensional world of polygons and how they experience the encounter with a 3 dimensional being.
In the diagram below (Diagram 2) we can see how the dimensions progress from 0 dimensions (0D) to 4 dimensions (4D). In 0D there is just a point and no possible movement. You can see as you progress that for each dimension a new direction of movement is introduced.
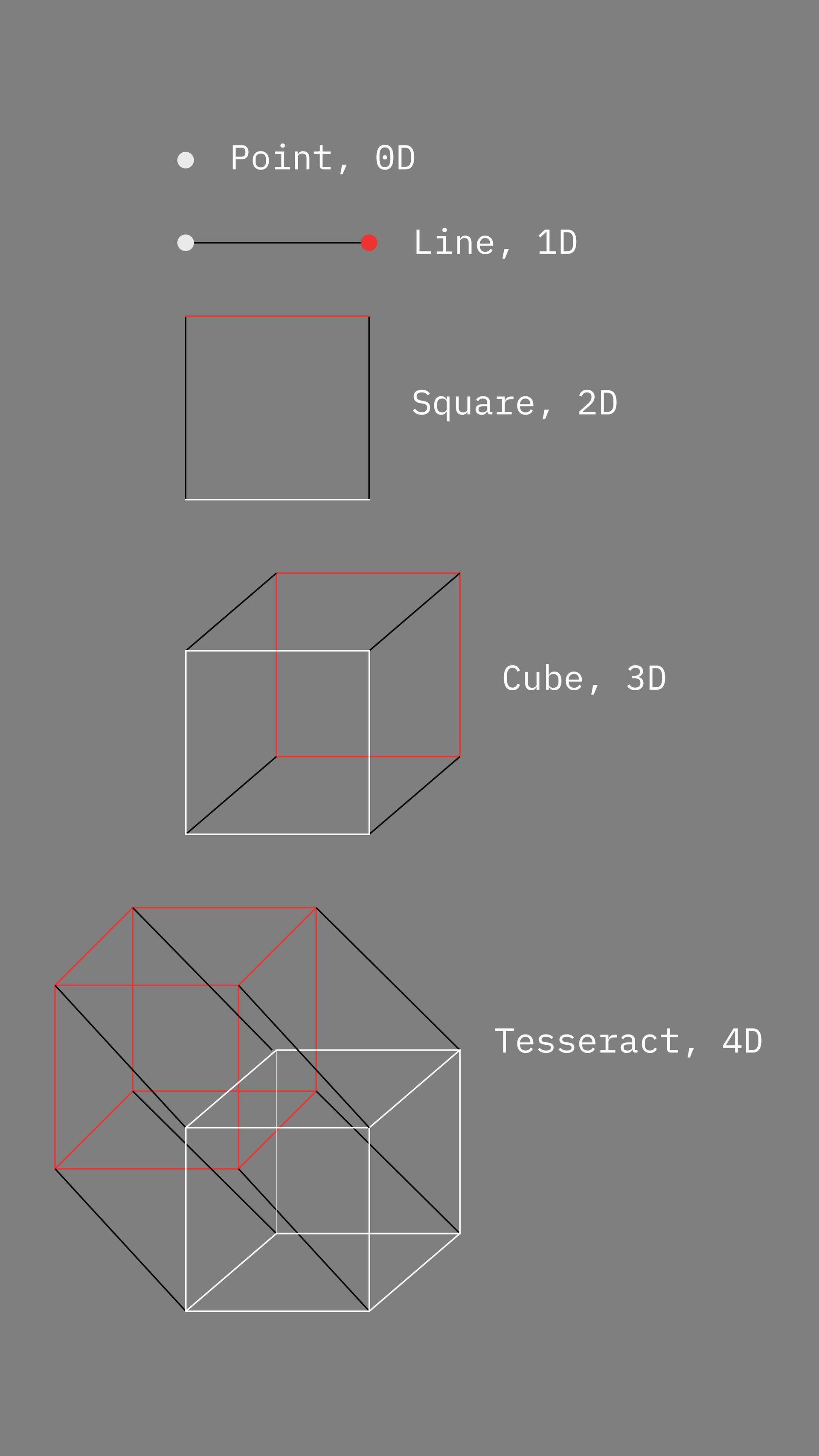
We generally refer to the horizontal direction as X. In 1 dimension there is a point which moves 1 unit in the X direction to create a line.
In 2 dimensions the line moves 1 unit in the vertical direction Y to form a square.
In 3 dimensions the square moves 1 unit in the forwards/backwards direction Z to form a cube.
And in 4 dimensions the square moves in the W direction, sometimes referred to as ana/kata, to form a 4D hypercube (tesseract).
These ideas are fundamental to what we know as Euclidean geometry which is based on 5 axioms. Two easily understood axioms and of particular import to multi-dimensional geometry are: the parallel postulate that 2 parallel lines shall never meet and the postulate that all right angles are equal, which means we can consider any number of mutually perpendicular axes.
Mysticism, religion and transcendence
It has been suggested that the late development of this field of geometry could be attributed to the idea that it was against nature to explain the world through ideas that could not be observed. One of the early twentieth century proponents of this new geometry H.P. Manning (1914) has written about this reluctance to recognise this geometry and R. Rucker (1985) examined how the Victorian mathematicians and theologians also speculated on the existence of God as an omnipotent being in an infinite dimension.
C.H. Hinton (b.1856 – d.1932) took these extrapolations further to an almost evangelical extreme with a multi-dimensional set of beliefs and philosophy in his writings, publishing a series of pamphlets ‘Scientific Romances’ (1884) and ‘The Fourth Dimension’ (1904). His works have been examined in depth by E. L.Throesch (2019) in her book Before Einstein: The Fourth Dimension in Fin-de-Siècle Literature and Culture.
Art and the fourth dimension – a springboard for the imagination

Of significance to the history of art and something which according to L. Henderson (1984) has been overlooked in Twentieth Century Art History is the effect that alternative geometries had on art at the turn of this century. She makes very significant claims in particular to the influence of n-dimensional geometry.
Specifically, belief in a fourth dimension encouraged artists to depart from visual reality and to reject completely the one-point perspective system that for centuries had portrayed the world as three-dimensional. (Henderson 1984, p.205)
My thesis ‘Impossible Worlds’ briefly examines this relationship in the context of the computer as a new medium. For an in-depth study Linda Herderson’s, 'The Fourth Dimension and Non-Euclidean Geometry in Modern Art' (1983) is the seminal text-book on this subject.
Picasso was given Esprit Jouffret’s book Traité élémentaire de géométrie à quatre dimensions (Elementary Treatise on the Geometry of Four Dimensions, 1903) and it is said that his portrait of Daniel-Henry Kahnweiler bears similarities to Jouffret’s drawings.

The 11th dimension
Just as we can extrapolate from two dimensions to three and onto four, we can keep going all the way to eleven – which some Victorian theologians believed was the domain of God.
There are 2048 vertices, 28,160 squares, 42,240 cubes and 42,240 4D hypercubes (tesseracts) in a 11D hypercube (hendekdekeract).
But why stop at 11?
Hypercubes in virtual reality
Having developed the software for display on desktop and made the artwork for augmented reality it was a small step to make a version that can be viewed in a VR headset.
If your device supports VR you can experience a stereoscopic rotating hypercube here: https://m-i-t-a.github.io/inscription4d-vr-public/
‘into and out of' – construction of the augmented reality hypercube
The development of this artwork involved the combination of various web technologies. The widespread use of smart phones with cameras with increasingly fast processors is key but also the adoption of open web standards and the availability of open-source software.
The software is browser based which means it can be linked to with a simple QR code pointing to a website url.
The two key open-source software libraries:
1. MindAR.j https://github.com/hiukim/mind-ar-js – this is the augmented reality component that allows the phone camera to detect the presence of Kimsooja’s Bottari image and then create an anchor on which the content can be attached
2. Three.js https://threejs.org/ – a framework for 3 dimensional visualisation
The multi-dimensional software is code that I have developed using the fundamentals from my MA project and required migrating the old code from the C programming language to modern Javascript. The hypercubes are projected from 4D to 3D, at which point the Three.js software is able to handle the rendering to 2D for screen display.
The rest of the technology stack is fundamental and common to modern website development.
It is hoped that the new open standard WEbXR https://developer.mozilla.org/en-US/docs/Web/API/WebXR_Device_API will soon become widely supported. This will afford greater flexibility, faster speed and more functionality.
I intend that WebXR will replace the MindAR.js component in the software when it becomes widely supported. It should be faster and enable more flexibility in the control of the AR experience.
At the time or writing MindAR.js is widely supported on different devices and browsers and is the best option tested for image tracking.
Appendix A: bibliography
- Abbott E.A. (1884) Flatland: A Romance of Many Dime11sions, Dover, New York, 1992, first published Seeley &Co. Ltd., London (1884)
- Ascott R. (1990) Is There Love in the Telematic Embrace?, Art Journal, Fall, pp.241- 247
- Axelrod R. (1990) The Evolution of Cooperation, Penguin, London
- Banchoff T. and Cervone D.P. (1990) Illustrating 'Beyond the Third Dimension',Leonardo, Vol.25, No.4, pp.273-280
- Banchoff T. (1990) Beyond The Third Dimension, Scientific American Library, New York
- Beyls P. (1991) Discovery through Interaction: A Cognitive Approach to Computer Media in the Visual Arts, Leonardo, Vol. 24, o.3, pp.311-315
- Binkley T. (1990) The Quickening of Galatea: Virtual Creation without Tools or Media, Art Journal, Fall
- Bragdon C. (1915) Projective Ornament, first published Rochester, New York: The Manas Press
- Brisson D.W. (1978) Hypergraphics: Visualizing Complex Relationships in Art, Science and Technology, Westview Press Inc., Colorado
- Brisson H. (1992) Visualization in Art and Science, Leonardo, Vol.25, No. 3/ 4, pp. 257-262
- Brown P. (1990) Steps Toward the Evolution of a New Medium: Computer-Aided Art and Design, Leonardo, Vol. 23, No. 2/3, pp. 201-207
- Bruce B. (1993) Virtual War, The Face, o.55, April 1993, pp.104-111, 125 Clauser H.R. (1988)
- Towards a Dynamic, Generative Computer Art, Leonardo, Vol.21, No. 2/3, pp. 115-122
- Costa M. (1991) Technology, Artistic Production and the 'Aesthetics of Communication', Leonardo, Vol. 24, No. 2, pp. 123-125
- Coxeter H.S.M. (1973), Regular Polytopes, Dover, New York
- Dee J. (1977) Four Space: a Forgotten Dimension of the Mind, Brampton: LYC Museum, Cumbria
- Duchamp M. (1967) The White Box notes, ‘à l’infinitif’, Richard Hamilton, 1999
- Earnshaw RA., Gigante M.A. and JONES H. (1993) Virtual Reality Systems, Academic Press, London
- Forest F. (1991) Aesthetics and Telecommunications Systems, Leonardo, Vol. 24, No. 2, pp. 137-138
- Franke H.W. (1987) The Expanding Medium: The Future of Computer Art, Leonardo, Vol. 20, No. 4, pp. 335-338
- Gardner M. (1971) Mathematical Games - On cellular automata, self-reproduction, the Garden of Eden and the game of "life", Scientific America, February, pp. 112-117
- Gibson W. (1986) Neuromancer, London, Grafton
- Gidney E. (1991) Art and Telecommunications - 10 Years On, Leonardo, Vol. 24, No.2, pp. 147-152
- Gunn C. and Maxwell D. (1992) Not Knot, Der Prix Ars Electronica, Die Deutsche Bibliotec
- Henderson L.D. (1983) The Fourth Dimension and Non-Euclidean Geometry in Modern Art, Princetown University Press, New Jersey
- Hinton, C. H. (1906), The Fourth Dimension, first published Swan Sonnenschein and Co, London
- Kruger M.W. (1991) Artificial Reality II, Addison-Wesley, U.S.A.
- Mallary R. (1969) Computer Sculpture: Six Levels of Cybernetics, Artforum, Fall
- Mallary R. (1990) Spatila-Synesthetic Art through 3-D Projection: The Requirements of a Computer-Based Supermedium, Leonardo, Vol. 23, No. 1, pp. 3-16
- Manning H.P. (1910) The Fourth Dimension Simply Explained: a collection of essays selected from those submitted in the Scientific America's prize competition, Munn & Company, Inc., New York
- Manning H.P. (1914) Geometry of Four Dimensions, The MacMillan Company, New York
- Pimentel K. and Teixeira K. (1993) Virtual Reality: Through the New Looking Glass, Wildcrest Books, USA
- Robbin T. (1984) Painting and Physics: Modelling Artistic and Scientific Experience in Four Spatial Dimensions, Leonardo, Vol. 17, No. 4, pp.227-233
- Rheingold H. (1991) Virtual Reality, Secker and Warburg, London
- Rucker R. (1986) The Fourth Dimension and How to Get There, Penguin, London
- Throesch E. L. (2019) Before Einstein: The Fourth Dimension in Fin-de-Siècle Literature and Culture, Anthem Press, London and New York
- Whitney J. Snr. (1991) Fifty Years of Composing Computer Music and Graphics: How Time's New Solid-State Tractability Has Changed Audio-Visual Perspectives, Leonardo, Vol. 24, No. 5, pp. 597-599
- Wilson S. (1991) Noise on the Line: Emerging Issues in Telecommunications-Based Art, Leonardo, Vol. 24, No. 2, pp. 175-177
- Woolley B. (1992) Virtual Worlds: A Journey in Hype and Hyperreality, Blackwell, Oxford
- Zajec E. (1978) Computer Art: A Binary System for Producing Geometrical Non Figurative Pictures, Leonardo, Vol. 11, pp. 13-21 B. Technical resources
Appendix B: technical resources
i. MindAR
MindAR is a web augmented reality library
https://github.com/hiukim/mind-ar-js
Medium article: develop a web augmented reality app with MindAR in 5 minutes!
Documentation
https://hiukim.github.io/mind-ar-js-doc/
ii. Three.js
Cross-browser, general purpose 3D library
Three.js custom BufferGeometry
https://r105.threejsfundamentals.org/threejs/lessons/threejs-custom-buffergeometry.html
How to create VR content
https://threejs.org/docs/#manual/en/introduction/How-to-create-VR-content
iii. WebXR
WebXR Device API is a web application programming interface (API) that describes support for accessing augmented reality and virtual reality devices
https://developer.mozilla.org/en-US/docs/Web/API/WebXR_Device_API
WebXR experiments
https://shirinstar.github.io/webAR_experiments_page/
WebXR Experiments source code
https://github.com/ShirinStar/webAR_experiments
WebXR image tracking API - explainer
https://github.com/immersive-web/marker-tracking/blob/main/explainer.md
Medium article part 1 and 2: Three.js and WebXR getting started
Image tracking with WebXR
https://www.youtube.com/watch?v=9LwTDKWC9G0
iv. Other AR technologies
ARCore - augmented images https://developers.google.com/ar/develop/augmented-images
AR.js
https://ar-js-org.github.io/AR.js-Docs/image-tracking/
v. Javascript tips and techniques
Touch input
https://web.dev/mobile-touchandmouse/
vi. Debugging and testing
Remote debugging
https://developer.chrome.com/docs/devtools/remote-debugging/
chrome://inspect/#devices
WebXR image tracking example
Enable WebXR Incubations
chrome://flags/
vii. VR
WebXR headsets
https://aframe.io/docs/1.3.0/introduction/vr-headsets-and-webxr-browsers.html


